, or Lobachevskian geometry,
describes a space of constant negative curvature. Two “straight lines” which do not intersect are diverging
more and more in both directions; the sum of interior angles of any triangle is less than 180°.
The Poincaré disk

The two-dimensional space of positive curvature is a sphere. In contrast, the two-dimensional space of negative curvature
is infinite and doesn't have a real-world analogy. One of the possible ways to “look” at this space and analyze it
is the
Poincaré disk model. It is a mapping
between the infinite two-dimensional hyperbolic space and a finite flat disk (placed on a conventional Euclidean plane).
“Straight lines” of the hyperbolic space appear in the Poincaré disk as arcs, and images of identical objects have
different sizes. The boundary of the disk represents points which are infinitely far away.
Polygonal tiling
The Euclidean plane can be
tiled with hexagons,
which results in a honeycomb. One can't use heptagons or octagons the same way: they “don't fit”. But in the hyperbolic
space it is possible. For example, one can fill the whole infinite space with non-overlapping octagons. In the Poincaré
disk representation the octagons appear distorted and having different size, but “actually” they are all identical
and separated by “straight lines”.
If other curves are used instead of straight lines, octagons transform into intricate shapes.
It is possible to embed a bird figure into the octagon. Appropriate choice of the shape and relative placement of birds allows
combining them without overlapping and gaps.
It turns out that some birds “look in a different direction” compared to others, in other words, some birds are
mirror reflections of other ones. This fact can be used to choose different colors, for example, by painting each bird either
in orange or in blue.
Then, it's possible to differentiate each set of birds into different shades of orange and blue so that adjacent birds
always have different colors.
User interaction: moving the Poincaré disk
The center of the Poincaré disk can be “aimed” at an arbitrary location in the hyperbolic space. This
affects the resut of the transformation: which objects are shown at the center and appear large, and which objects are shown near
the boundary and appear smaller. Moving the Poincaré disk over the hyperbolic space, or, in other words, “scrolling”
the space under the disk, produces a continuous animation.
Using WebGL
The
WebGL technology allows creating high quality real-time
animations which employ hardware 3D acceleration (OpenGL). WebGL is supported in all modern Web browsers, allowing 3D graphics
to be used on Web sites without having to install anything on the computer.
This demonstration uses only one bird image. A dedicated
shader (small program executed on the video card) reproduces this
image in different colors and transforms these copies according to the Poincaré disk formulae. When the user moves the image using
the mouse or finger, the script recalculates this into the Poincaré disk motion over the hyperbolic space and sends these values to
the video card. Since the final image is generated on the video card, it is possible to display a sophisticated animation in real time
without performance limitations imposed by conventional scripts.
And still this reminds me of something...
Of course, this demonstration was inspired by the works of M.C. Escher.
The Dutch graphic artist
Maurits Cornelis Escher was
interested in the beauty of mathematics and geometry. In particular, some of his paintings show tilings of
the hyperbolic plane transformed using the Poincaré disk, the most famous being
Circle Limit III and
Circle Limit IV. Escher was also replacing
regular polygons by various shapes such as fishes, lizards, angels and demons.
I have deliberately used a complex and asymmetric image of a bird in this demonstration, therefore the resulting image is
quite intricate and the symmetry is not apparent. In Escher's pictures the symmetry is always obvious and it is not too hard to
determine which polygons it is based on.
Also, Escher was drawing his pictures by hand (or even carving them on wood) and could not use computer animation.
Where can I see more animated works of Escher?
Dutch mathematicians have analyzed the Escher's drawing
“
Print Gallery” in 2013
on their site. In 2009 a Swedish programmer implemented
their algorithm
in WebGL; a Dutch programmer developed
another WebGL implementation in 2014.
The site of another Swedish programmer features an interactive demonstration where one can create and move
interactive tilings of the hyperbolic plane displayed
using the Poincaré disk transformation. The site also has a lot of materials about the
hyperbolic geometry. Another interactive demonstration allows to
turn a regular polygonal tiling of the Euclidean plane into
arbitrary shapes.
Return to demonstration
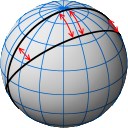 Spherical geometry, or Riemannian geometry,
describes a space of constant positive curvature, such as the surface of a sphere. Great circles, such as the equator
and meridians, are used as straight lines. Any two “straight lines” are eventually intersecting;
the sum of interior angles of any triangle exceeds 180°.
Spherical geometry, or Riemannian geometry,
describes a space of constant positive curvature, such as the surface of a sphere. Great circles, such as the equator
and meridians, are used as straight lines. Any two “straight lines” are eventually intersecting;
the sum of interior angles of any triangle exceeds 180°.
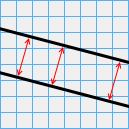 We all know the “usual” Euclidean space where parallel lines never intersect and are always at the same distance
from each other. The two-dimensional Euclidean space is called a plane.
We all know the “usual” Euclidean space where parallel lines never intersect and are always at the same distance
from each other. The two-dimensional Euclidean space is called a plane.
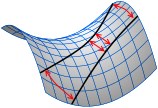
 The two-dimensional space of positive curvature is a sphere. In contrast, the two-dimensional space of negative curvature
is infinite and doesn't have a real-world analogy. One of the possible ways to “look” at this space and analyze it
is the
The two-dimensional space of positive curvature is a sphere. In contrast, the two-dimensional space of negative curvature
is infinite and doesn't have a real-world analogy. One of the possible ways to “look” at this space and analyze it
is the 






