, или гиперболическая геометрия,
описывает пространство постоянной отрицательной кривизны. Если две «прямые» не пересекаются, то они расходятся
всё дальше и дальше друг от друга; сумма углов любого треугольника меньше 180°.
Диск Пуанкаре

Двумерное пространство Римана – это сфера. А вот двумерное пространство Лобачевского является бесконечным и
не имеет наглядных аналогов. Один из способов «заглянуть» в пространство Лобачевского и изучать его –
диск Пуанкаре. Это отображение бесконечного двумерного пространства
Лобачевского в конечный плоский диск (находящийся на обычной, евклидовой плоскости). «Прямые линии» в пространстве
Лобачевского выглядят в диске Пуанкаре как дуги, а одинаковые объекты кажутся разного размера. Граница диска изображает точки,
находящиеся бесконечно далеко.
Заполнение многоугольниками
Евклидову плоскость можно
плотно заполнить шестиугольниками,
получатся пчелиные соты. Семиугольники или восьмиугольники так разместить не получается – они «не помещаются».
Но в пространстве Лобачевского это возможно. Например, можно заполнить всё бесконечное пространство восьмиугольниками, которые
не будут накладываться друг на друга. На изображении через диск Пуанкаре восьмиугольники кажутся разными и искривлёнными, но
«в действительности» они все одинаковые и состоят из «прямых линий».
Если вместо прямых линий использовать изогнутые отрезки, то можно превратить восьмиугольники в более сложные фигуры.
В восьмиугольник можно вписать фигуру птицы. Если правильно подобрать форму и взаимное расположение фигур, то их можно
совместить друг с другом без промежутков и наложений.
При размещении птиц оказывается, что некоторые птицы «смотрят в другую сторону», то есть одни птицы являются зеркальными
отражениями других. Можно использовать этот факт и раскрасить птиц в разные цвета, например, одних в оранжевый, а других
в синий.
Затем, можно раскрасить каждое множество птиц в разные тона оранжевой и синей гаммы, чтобы соседние птицы были разных цветов.
Интерактивность: перемещение диска Пуанкаре
При использовании диска Пуанкаре можно «направить его центр» в разные точки пространства Лобачевского. Результат
отображения будет разный: от этого зависит, какие объекты будут изображены в центре диска и будут казаться большими, а какие, наоборот,
окажутся ближе к краю и будут казаться уменьшенными. Двигая центр диска Пуанкаре по пространству Лобачевского, или, что то же самое,
«прокручивая» пространство под диском, можно получить непрерывную анимацию.
Использование WebGL
WebGL – технология, позволяющая создавать высококачественные анимации в реальном
времени, используя возможности аппаратного 3D-ускорения (OpenGL). Поддержка WebGL реализована во всех современных веб-броузерах, что
позволяет использовать 3D-графику в Интернете без необходимости что-либо дополнительно устанавливать на компьютер.
Приведённая здесь демонстрация использует всего одно изображение птицы. Специальный
шейдер (алгоритм, исполняемый на видеокарте) размножает это изображение, искривляет
его согласно формулам диска Пуанкаре и перекрашивает в разные цвета. Когда пользователь двигает изображение мышкой или пальцем, скрипт
вычисляет смещение диска Пуанкаре и отправляет эти значения в видеокарту. Поскольку рисование изображения производится на видеокарте,
можно отображать сложную анимацию в реальном времени, не ограничиваясь скоростью работы обычных скриптов.
И всё-таки это мне что-то напоминает...
Разумеется, на создание этой демонстрации меня вдохновило творчество Эшера.
Голландский художник
Мауриц Корнелис Эшер интересовался
художественной стороной математики и геометрии. В частности, несколько его картин изображают разбиение пространства Лобачевского
с помощью диска Пуанкаре, самые известные из них –
Circle Limit III
и
Circle Limit IV. Эшер тоже заменял правильные многоугольники сложными фигурами – рыбами, ящерицами, ангелами и демонами.
В моей демонстрации намеренно использована более сложная и асимметричная фигура птицы, поэтому в общем результате симметрия
получилась довольно сложная и на первый взгляд незаметная. В картинах Эшера симметрия всегда наглядна, и нетрудно определить,
на каких многоугольниках она основана.
Ну и ещё Эшер рисовал свои картины вручную (или даже вырезал на дереве) и, конечно, не мог использовать компьютерную анимацию.
Где бы ещё посмотреть анимированные картины Эшера и ещё что-нибудь похожее?
Голландские математики проанализировали картину Эшера
«
Картинная галерея» в 2003 году
на
своём сайте. В 2009 году шведский программист реализовал их алгоритм
с помощью WebGL; в 2014 году голландский программист создал
другую WebGL-реализацию.
На сайте другого шведского программиста можно создавать и двигать интерактивные
разбиения гиперболической плоскости, отображённые с помощью диска Пуанкаре, а также почитать
много интересного про геометрию Лобачевского.
Другая демонстрация позволяет разбиение евклидовой плоскости на правильные многоугольники
превратить в произвольные фигуры.
К демонстрации
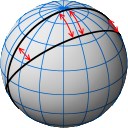 Геометрия Римана, или сферическая геометрия, описывает
пространство постоянной положительной кривизны, например, поверхность сферы. Роль прямых линий здесь выполняют большие
круги, такие как экватор и меридианы. Любые две «прямые» рано или поздно пересекаются; сумма углов любого
треугольника больше 180°.
Геометрия Римана, или сферическая геометрия, описывает
пространство постоянной положительной кривизны, например, поверхность сферы. Роль прямых линий здесь выполняют большие
круги, такие как экватор и меридианы. Любые две «прямые» рано или поздно пересекаются; сумма углов любого
треугольника больше 180°.
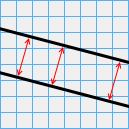 Мы все привыкли к «обычному» евклидову пространству, где параллельные прямые никогда не пересекаются и всегда
остаются на одинаковом расстоянии друг от друга. Двумерное евклидово пространство называется плоскостью.
Мы все привыкли к «обычному» евклидову пространству, где параллельные прямые никогда не пересекаются и всегда
остаются на одинаковом расстоянии друг от друга. Двумерное евклидово пространство называется плоскостью.
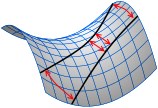
 Двумерное пространство Римана – это сфера. А вот двумерное пространство Лобачевского является бесконечным и
не имеет наглядных аналогов. Один из способов «заглянуть» в пространство Лобачевского и изучать его –
Двумерное пространство Римана – это сфера. А вот двумерное пространство Лобачевского является бесконечным и
не имеет наглядных аналогов. Один из способов «заглянуть» в пространство Лобачевского и изучать его –







